Twitterでみつけた面白いツイートを取り上げる.こういうのを考え付く人って凄い!天才!!尊敬する!!!
tweet
空ってどこら辺からどこら辺までの人が同じの見てるんだろう
— 相羽 ういは ????(あいばういは)@にじさんじ (@AibaUiha) July 27, 2021
問題
円C:\(x^2 + y^2 = r^2 \)( \(r \lt 0\) )を \(x\) 軸を中心にして回転させた球体を考える. \(x\) 軸上の点P(\( p, 0\))(\( p \lt r \))から球体に光を当てた際に光が映る部分の面積を求めよ.
解答例
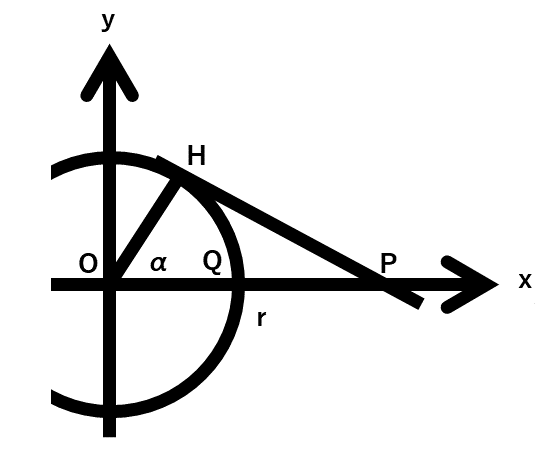
点Pから円Cに引いた接線について,第1象限にある接点を点H(\(r \cos \alpha, r \sin \alpha\))(ただし,∠POH\(=\alpha, 0 \lt \alpha \lt \displaystyle\frac{\pi}{2} \))とおく.
また,線分OPと \( x \) 軸との交点を点Q(\(r, 0\)) とおく.
求めるべき面積をSとすると,Sは円弧HQを \( x \) 軸を中心に回転させたものとなる.
△POHは∠OHP \( = \displaystyle\frac{\pi}{2} \) の直角三角形なので,\(\displaystyle \cos \alpha = \frac{\mathrm{OH}}{\mathrm{OP}} = \frac{r}{p}\)
また,円Cは,第1象限において\( (x, y) = (r\cos \theta, r \sin \theta) \) (\(0 \lt \theta \lt \displaystyle\frac{\pi}{2}\))と表せる.
したがって,求める面積は \[\begin{eqnarray} S &=& \int_{\theta = 0}^{\theta = \alpha} (2 \pi y \cdot r d \theta) \\ &=& \int_{\theta = 0}^{\theta = \alpha} 2 \pi r^2 \sin \theta d \theta \\ &=& 2 \pi r^2 (1 - \cos \alpha) \\ &=& \frac{2 \pi r^2 (p-r)}{p} \end{eqnarray}\] となる.